

The paper can be found here - a highly recommended read!
In simple words: While the concept of timing is fundamental to our day-to-day lives, it has to be carefully examined in the world of distributed systems. This paper talks about exactly that. The objective here is three-folds:
* Discuss that the happened before relation on events in a distributed system is a partial order
* Method to synchronize system of logical clocks and henceforth define total ordering of events
* Using it to synchronize physical clocks
The idea of time, which is derived from the order in which events occur, is very fundamental to our day-to-day lives. (Eg. something is said to occur at 3.15 if it happens after 3.15 in clock and before 3.16 in the clock). However, in distributed systems, often it is impossible to say that one of the two events occurred first. The relation “happened-before” is therefore only a partial relation in such a system.
Nonetheless, the following definition of the happened-before relation is such that all of us would agree to it:
Definition (happened-before relation -->): The relation -> on the set of events of a system is the smallest relation satisfying:
* If a and b are events in the same process, and if a comes before b, then a –> b
* If a is sending of a message by one process and b is reveipt of the same message by another process, then a –> b
* Transitivity: if a –> b and b –> c, then a –> c
Clearly, –> is neither reflexive nor symmetric.
(Intuitively: we can also think of this relation as the one saying that it is possible for event a to causally affect event b if a –> b)
Corollary: Two distinct events a and b are concurrent if a -/-> b and b -/-> a
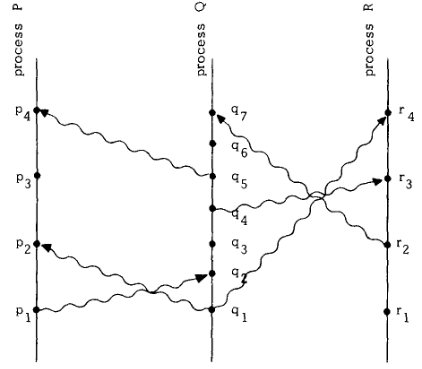
Consider the image above. It represents time in the vertical direction. The dots denote events and the wavy lines denote the messages. Clearly p1 –> r4 while p3 and q3 are concurrent. (Even though q3 appears to occur at an earlier physical time than p3, process P cannot know what process Q did at q3 until it receives the message p4.)
The author here describes a way to synchronize logical clocks across systems that will help us extend the above happened-before relation into a total order. This is just a way to assign numbers to our events, where the number can be thought of as time at which the event occurred.
Clock-Condition: For any events a,b if a –> b then C(a) < C(b)
Observe that the converse need not hold, since that would imply that any two concurrent events must occur at the same logical time.
Using the above system of logical clocks, it is rather straight forward to place a total ordering (==>) on the events. Simply, order the events by the time they occur at. To break ties, use arbitrary order of processes.
This total order relation is not unique. Different choices of clock yield different relations.
To solve this, we use logical clock described by IR1 and IR2 to define total ordering of events. With this ordering the slution is straightforward.
Assume the messages are received in order in which they are sent (this assumption can be avoided by introducing message numbers). Also that each process maintains its request queue hidden from others. Initially these contain T0:P0 where P0 is the process initially granted and T0 is less than any clock.
Tm:Pi to every other process and puts that message on its own request queue, where Tm is the timestamp of the message.Tm:Pi, it places it on its request queu and sends a (timestamped) ack to PiTm:Pi message from its request queue and sends a (timestamped) Pi release resource messageTm:Pi messages from its request queueTm:Pi in the request queue ordered before any other reuqest (b) Pi has received message from every other process timestamped later than TmConsider the following situation. Suppose a person issues request A on computer A and then telephones friend in another city to have him issue request B from PC B. It is possible for request B to receive a lower timestamp and be ordered before request A. This can happen because system has no way of knowing that A actually preceded B, since the precedence information is external to the system.
Let T be set of all system events. Let T1 be set of events in T along with external events. Let ~~>> denote happened-before relation in T1. There is no way for any alogrithm based solely on events of T to correctly order A before B since internal to system A -/-> B. So, in order to solve the anamolous behaviour, we can either ask the user to incorporate the external information into the system by explicitly assigning event B a timestamp greater than that of request A. The second approach is to construct a system of clocks that satisfies the following condition:
Strong Clock Condition: For any events a,b in T:
if a ~~» b then C(a) < C(b)
Note that this is not generally satisfied by our logical clocks. Let us identify T1 with some set of real events and let ~~>> be partial ordering of events in T1.
Ci(t) be the reading of clock Ci at physical time t (also assume Ci to be continuous except when we reset it)|dCi(t)/dt - 1| < k (i.e. Ci(t) runs at approximately the same rate as the physical time)|Ci(t) - Cj(t)| < e, for a small constant e (i.e. not all should all run at approximately the same pace, they should at all times be synchronized with each other - allowing a max tolerance parameter of e)T follow the strong clock condition.u > 0 be a constant less than the shortest transmission time for the interprocess messages. This means, for any event a and b, such that a occurs at physical time t and a ~~» b, then b must occur at a physical time later than t+uCi(t+u)-Cj(t) > 0 for any i,j,t. This condition along with PC1 and PC2 gives the inequality e <= (1-k)*u (See image below)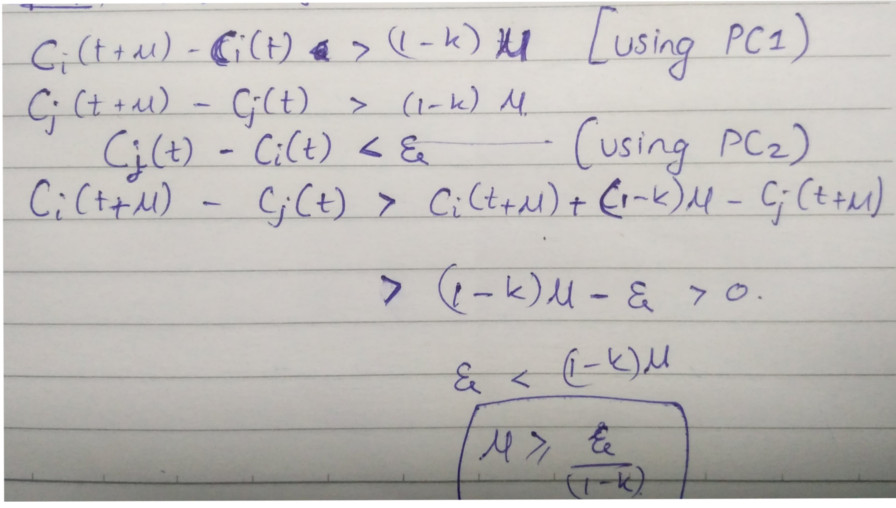
e<sub>m</sub>=vm-u = unpredictable delay of m.Change IR1 and IR2 to the following:
IR1: For each i, if Pi does not receive message at time t, then dCi(t)/dt > 0
IR2: (a) If Pi sends a message m at time t, then m contains timestamp Tm = Ci(t).
(b) Upon receiving m at time t1, process Pj sets Cj(t1) >= max(Cj(t1), Tm+u)
A very important point in the world of distributed systems is that the ordering of events is only a partial order. This idea is usefulin reasoning and thinking about distributed systems. The paper helps concretise the fact in our minds. Extending this to form a tolta order was relatively straight forward. Using this to synchronize the physical clocks is nice technique, since we don’t often realize how we get confused by such anomalous behaviour in our regular dealing with distributed systems.